一些个人的想法

小波等其实本质上是相关运算

首先自相关是最大值

互相关又是0，也就是正交

傅里叶变换拆分成每一小段也是小波基，本质上是一样的。

与傅里叶变换的关系：傅里叶变换的基是$\delta$函数，小波是其线性组合，一个例子是频域的窗是小波基。

信号拟合的特性

某一个信号是否能被还原

1. 频率越稀疏则时长需要很长。$\mathrm{\Delta }f=\frac{1}{T}$
2. 无限长的信号没有混叠，有限的有混叠。这个混叠也可以理解为窗的影响

等间距采样（全采样）

一般来说离散信号的拆分只要满足 $Nyquist$ 采样定律，也就是满足大于最高频信号的二倍频即可还原。图像压缩就是全采样后舍弃了小系数的内容。

不等间距采样（亚采样）

压缩感知直接进行了亚采样，然后再用算法消除亚采样导致的伪影。可以说，压缩感知直接在采样时就完成了压缩。 陶哲轩等人证明：独立同分布的高斯随机测量矩阵可以成为普适的压缩感知测量矩阵。

消除随机噪声

自相关，因为随机信号的正交特性。

卷积

图像的卷积

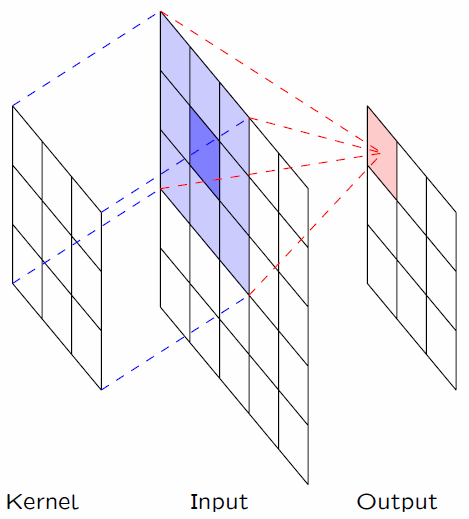
卷积示意图

卷积的过程就是滤镜/滤波的过程，比如一个 $3\times 3$ 的卷积核，

$$\left[\begin{array}{ccc}1/9& 1/9& 1/9\\ 1/9& 1/9& 1/9\\ 1/9& 1/9& 1/9\end{array}\right],$$

是模糊效果/低通滤波的效果。为了保证其能量不变，总和需要为1。 边缘检测/高通的卷积核为，

$$\left[\begin{array}{ccc}-1& -1& -1\\ -1& 8& -1\\ -1& -1& -1\end{array}\right],$$

这些卷积核也是一种小波

信号的卷积

信号的卷积类似于X+Y的概率，按照两个信号的共同作用时间 $t+(\tau -t)$ 来区分信号。

Z=X+Y这样的概率是概率函数的卷积，记为$f_z=f_x\ast f_y$。中心极限定理是同概率波形很多次卷积的结果。

内积-卷积-相关

若A为基，则内积是将能量分配到A上

$$B=\sum _n^{i=1}(B,A_i)A_i$$

对时域加窗（内积）就是对频域卷积，反之对频域加窗（滤波）就是对时域卷积。

$$⟨f,g⟩={\int }_R^{}f\cdot \overline{g}dx$$$$f\ast g=⟨f(y),g(x-y)⟩={\int }_R^{}f(y)\cdot g(x-y)dy$$

相关运算的公式如下

$$\begin{array}{rl}& \mathrm{相}\mathrm{关}：R(\tau )=⟨x(t),y(t-\tau )⟩\\ & \mathrm{卷}\mathrm{积}：C(\tau )=⟨x(t),y(\tau -t)⟩\end{array}$$

与内积对应的还有叉积：一种构造正交的方法，模为体积(或面积)
$a\times b=\left|\begin{array}{ccc}i& j& k\\ x_1& y_1& z_1\\ x_2& y_2& z_2\end{array}\right|$
当然也有一种经典的构造方法。$\xi$是辅助向量，我们将$\xi$的${\phi }_k$分量都删干净，依次构造：

首先确定${\phi }_0$
接下来${\phi }_n=\xi -\sum _{k=0}^{n-1}(\xi ,{\phi }_k)\cdot \frac{{\phi }_k}{\Vert {\phi }_k\Vert }$
一个例子是$\phi$取$x^n$，这样多项式空间就可以随便构造了
对应于数值分析原理Page151，书上还给出了一个递推公式用于构造多项式空间的正交多项式序列

带权内积

$$(f,g)=\int \rho \cdot f\cdot gdx$$

带权函数$\rho (x)=\{\begin{array}{ll}1& \text{ if }-1<x<1,\\ 0& \text{ else }\end{array}$的正交多项式称为Legendre多项式 : $P_0(x)=1,P_1(x)=x,P_2(x)=(3x^2-1)/2,...$
还有Laguerre、Hermite、Chebyshev等等
带权内积可用于多项式逼近，评价方式：函数的最佳平方逼近${\Vert f-\phi \Vert }_2^2$，${\Vert \cdot \Vert }_2$可以称为函数范数，这不就是二范数吗。
离散的最佳平方逼近为最小二乘问题，实际上就是将y向量投影到基上来计算系数，反之不也是用正交的基去逼近y向量吗。

TIP

拟合好的多项式函数还能拿来计算数值积分。

变换

各种变换都需要考虑收敛域，也各有不用的收敛条件，避免发散。

• 傅里叶变换

$$F(\omega )=⟨f(t),e^{-j\omega t}⟩$$

• 拉普拉斯变换($s=\sigma +j\omega$)，这里引入$\sigma$控制收敛情况，使其可以处理发散的一些函数，比如$t^n$，这样一般的常微分方程都可以用Laplace求解。

$$F(s)=⟨x(t),e^{-st}⟩$$

• Z变换($z=e^{st}=e^{(\sigma +j\omega )t}$)，为离散信号数列服务的通项公式。其中的留数等都是复变函数的知识。

$$X(z)=\sum _{n=0}^{\mathrm{\infty }}x(n)z^{-n}$$

概率论

• 期望：${\mu }_x=EX=⟨x_k,p_{x_k}⟩$
  举例： 若X服从$[a,b]$的均匀分布，则期望$EX=\frac{a+b}{2}$

• 极大似然估计：
  $$\begin{gathered} L({\theta }_1,...,{\theta }_m)\stackrel{def}{=}\prod _{i=1}^{n}f(x_i;{\theta }_1,...,{\theta }_m), \\ \mathrm{这}\mathrm{里}\mathrm{的}\theta \mathrm{可}\mathrm{以}\mathrm{是}\mu ,{\sigma }^2,\lambda \mathrm{等}\mathrm{等}\mathrm{概}\mathrm{率}\mathrm{模}\mathrm{型}\mathrm{的}\mathrm{参}\mathrm{数},\mathrm{使}\mathrm{满}\mathrm{足}lnL({\hat{\theta }}_1,...{\hat{\theta }}_m)\mathrm{最}\mathrm{大}，\mathrm{即}\frac{\partial lnL}{\partial {\theta }_j}=0 \end{gathered}$$求得驻点。

• 大数定理：频率$\to$概率

• 中心极限定理：独立同分布，有限方差和数学期望，则$\sum _{i=1}^n{X}_i$近似服从，$\mathcal{N}(n\mu ,n{\sigma }^2)$

• 贝叶斯公式：可以拿来训练神经网络，因为它可以从反向推正向概率。$\mathrm{设}{A}_i\mathrm{不}\mathrm{相}\mathrm{容}，A_1+...+A_n\supset B,\mathrm{则}P(A_i|B)=\frac{P(A_i)P(B|A_i)}{P(B)}$

• 瑞利分布：$X,Y\sim \mathcal{N}(0,{\sigma }^2),\mathrm{则}Z=\sqrt{X^2+Y^2}$的分布为瑞利分布

随机信号

• 平稳随机信号$X(n)$的概率密度函数对宽为N的信号都一致，称为N阶平稳
• 宽平稳随机信号满足均值常数、方差有限，且$r_x(n_1.n_2)=E[X(n)X(n+m)]=r_x(\mathrm{m}),\mathrm{其}\mathrm{中}\mathrm{m}=n_1-n_2$表示自相关函数仅与差值m有关
• 白噪声的自相关函数$r(m)={\sigma }^2\delta (m)$
• 自相关和卷积：

$$\begin{array}{rl}& Y(n)=X(n)\ast h(n)\\ & r_Y(m)=r_X(m)\ast h(m)\ast h(-m)\\ & \mathcal{F}[r_Y(m)]=P_Y=P_X|H{|}^2\end{array}$$

• 各态遍历信号，指样本可以遍历所有取值。这样就符合经典概率模型。也符合大数定理。此时的$r_x(m)=⟨x(n),x(n+m)⟩$。

附录

$(\overrightarrow{a},\overrightarrow{b})$表示向量内积，$⟨a,b⟩$表示信号内积。 对于向量而言，$(\overrightarrow{x},\overrightarrow{x})={\Vert \overrightarrow{x}\Vert }_2^2$表示2范数，范数满足三角不等式，就同绝对值的三角不等式一样。